By Dr. Gary Deel
Faculty Director, School of Business, American Public University
This is the second of three articles examining the role that global positioning systems (GPS) play in modern transportation. Check out parts one and three.
The modern global position system (GPS) has revolutionized the way we locate and navigate everything from the family SUV to the jumbo jets crisscrossing the international airways. As such, we often take this invaluable tool for granted – that is until we know how it works.
Get started on your Space Studies Degree at American Military University. |
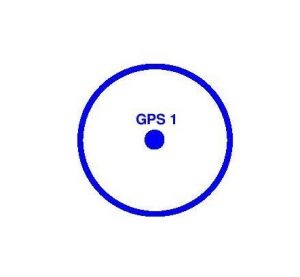
Once a GPS satellite knows the distance between it and a GPS device on the Earth, it can map a sphere around itself. The sphere represents all potential locations where the ground-based device might be. Hypothetically, the GPS device could be anywhere on this sphere because the satellite is incapable of determining the direction from which the signal was measured.
However, it can make some educated inferences based on its programming. The sphere would necessarily overlap with the surface of the Earth below the satellite. But some of the points on the sphere would actually be beneath the surface. And many more still would be out in space in every direction that the Earth is not.
Obviously, a GPS device will not be buried inside the Earth’s crust. Similarly, a GPS device will not be floating in outer space. Therefore, the actual sphere of potential locations can be reduced to a ring of points where the sphere intersects with the Earth’s surface.
This ring is more or less smooth and consistent. In reality, however, the GPS system must allow for a certain amount of variability to account for potential differences in altitudes on the Earth’s surface. The most obvious source of these differences would be changes in the elevation of landmasses.
GPS Must Consider whether a Device Might Be Pinging from an Ocean or a Mountain
GPS must be able to account for whether a device might be pinging from the middle of an ocean (i.e. at sea level) or from the top of a mountain. This means deviations in altitude. Other artificial sources of altitude changes include GPS devices in airplanes, tall buildings, and in.
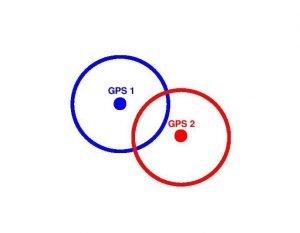
But even if the ring were perfectly flat and consistent, there is another problem: That ring includes a nearly infinite number of location points where the GPS device could be. So, to pinpoint its precise location, GPS enlists the help of multiple satellites. Instead of one satellite mapping one ring of potential points on the surface of the Earth, imagine two satellites mapping two rings.
It is technically conceivable that—if the two satellites are in just the right locations, they might intersect at only one point (picture two circles forming an 8). But realistically, it is much more likely that the rings would overlap to some degree, as pictured in the illustration above. In that case, the rings would intersect at two points. Thus, an infinite number of potential location points for the GPS device would be reduced to just two.
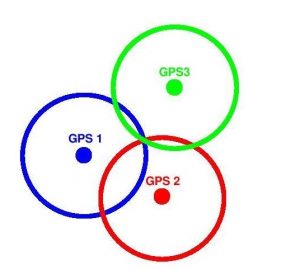
Of course, two still are not good enough. When a user looks to a smartphone for navigation, the GPS system does not provide two hypothetical sets of directions from which to choose. It narrows the location of the device to one possible site, which it does through the addition of a third satellite. This is called trilateration. (As a side note, this is often incorrectly confused with the word “triangulation,” which refers to the measurement of angles, not distances.)
By using a third satellite to map a ring on the surface of the Earth, there can be one and only one point where all three rings intersect. As such, the GPS network can pinpoint the device’s location. Although it takes a minimum of three satellites to do the job, in reality, modern GPS networks might actually use more than three satellites to lock down a device’s location. Each additional satellite adds a greater level of accuracy by limiting potential uncertainty along different axes in three-dimensional space.
GPS Requires Enough Satellites in Orbit So One Is Always Overhead when Location Data Is Needed
The process GPS uses to provide location and navigation data may sound straightforward, but it is actually quite complicated. For one, it requires enough satellites in orbit so that one is always overhead when an Earth-bound device requests GPS location data. It also requires that the orbiting satellites and the devices on the ground are equipped with omnidirectional antennas so that pointing and precision alignments are not necessary for GPS communication.
Clocks on the Satellites and on the Ground Must Be Precisely Calibrated and in Sync
Finally, in order for GPS to make an accurate assessment of time intervals for signal transmissions, the clocks on the satellites and those on the ground must be precisely calibrated and in sync. If the clocks are off by even a little, the time interval for the signal transmission cannot be accurately assessed and the distance cannot be accurately measured.
Fortunately, modern technology has provided ways to accurately keep time using atomic clocks. However, when the first satellites went into orbit, an even greater obstacle was discovered, which threatened mission controllers’ ability to keep time synchronized on Earth and in space. The problem is called time dilation, and it was first posited by Albert Einstein in his general and special theories of relativity.
Einstein theorized that as an object’s speed increases, time for the object slows down. This may sound like something out of a science fiction story, but this is a real phenomenon. Time dilation occurs at any speed, but for humans used to traveling a few dozen mph in cars to a few hundred mph in airplanes, the effect is negligible. It is only when objects begin to really move (approaching the speed of light) that the differences become pronounced.
I actually wrote a previous article about the eeriness of this phenomenon when stretched to its ultimate consequences. At the limits of speed in our universe, time dilation could mean differences of years in the rate of time passage between slower-moving and faster moving objects.
What does this mean for GPS satellites? In the final part of this article, we’ll look at how time dilation threatened to undermine the entire global positioning project, and how engineers solved this problem with a clever workaround.
About the Author
Dr. Gary Deel is a Faculty Director with the School of Business at American Public University. He holds a JD in Law and a Ph.D. in Hospitality/Business Management. He teaches human resources and employment law classes for American Military University, the University of Central Florida, Colorado State University and others.

Comments are closed.